Création d'une Hélicoïde à pas variable en utilisant la fonction "Courbe par équation"

Pour bien commencer l'année 2014, et rattraper un peu le retard pris sur le blog en fin d'année 2013, nous vous proposons aujourd'hui un petit "Trick" Inventor, visant à créer une hélicoïde à pas variable en utilisant la fonction "courbe par équation".

Commencez par créer une nouvelle esquisse 3D.

Voici maintenant des équations d'exemple que vous pouvez utiliser dans la fonction "Courbe par équation" afin de créer une courbe hélicoïdale:

En coordonnées cartésiennes:

x(t) = rayon * sin(360 * nb_tours * t)

y(t) = rayon * cos(360 * nb_tours * t)

z(t) = hauteur * t

      = nb_tours * pas * t

En coordonnées cylindriques:

r(t) = rayon

theta(t) = 360 * nb_tours * t

z(t) = (idem qu'en coordonnées cartésiennes)

------------------------------------------------

Voici maintenant quelques exemples réalistes obtenus à partir de la fonction Courbe par équation et en utilisant l'une de ces fonctions.

pour les 4 exemples les valeurs suivantes ont été utilisées:

rayon = 3 ou 3 * t

nb_tours = 5

hauteur = 10

pas = 2 ou 2 * t

t variant entre 0 et 1

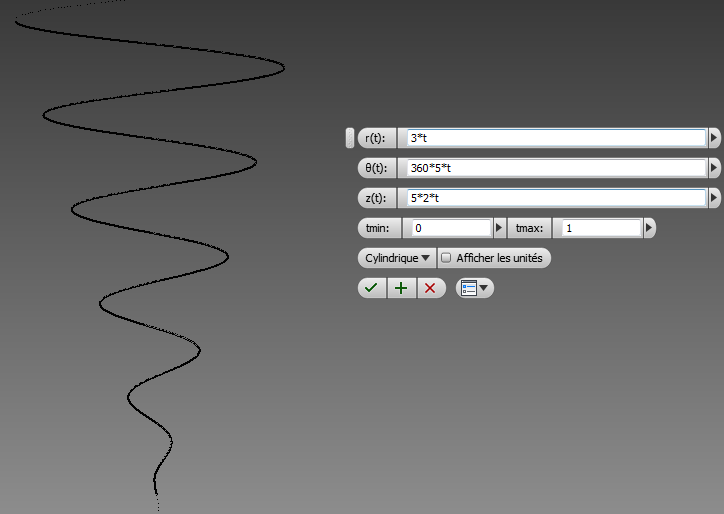
1. rayon constant et pas constant:

x(t) = 3*sin(360 * 5 * t)                                   r(t) = 3

y(t) = 3*cos(360 * 5 * t)                                  theta(t) = 360*5*t

z(t) = 5*2*t                                                    z(t) = 5*2*t           

2. rayon constant et pas variable:

x(t) = 3*sin(360*5*t)                                       r(t) = 3

y(t) = 3*cos(360*5*t)                                      theta(t) = 360*5*t

z(t) = 5*2*t*t                                                 z(t) = 5*2*t*t

3. rayon variable et pas constant:

x(t) = 3*t*sin(360*5*t)                                   r(t) = 3*t

y(t) = 3*t*cos(360*5*t)                                  theta(t) = 360*5*t

z(t) = 5*2*t                                                  z(t) = 5*2*t

4. rayon variable et pas variable:

x(t) = 3*t*sin(360*5*t)                                   r(t) = 3*t

y(t) = 3*t*cos(360*5*t)                                  theta(t) = 360*5*t

z(t) = 5*2*t*t                                                z(t) = 5*2*t*t